因果革命:人工智慧的大未來(書名翻譯的不好/畫蛇添足)
The Book of Why: The New Science of Cause and Effect
這本書的學術含金量超高,回顧過去百年來的統計與因果觀點爭辯
第六章破解悖論!
悖論的出現
1.人腦把相關性解釋成因果,但資料與事件分配遵守機率與比例邏輯
2.誤把某個領域學到的邏輯法則,套用到另一個領域
令人費解的蒙提霍爾問題
假設你參加一個遊戲節目,你被要求在三扇門中選擇一扇:其中一扇後面有一輛車;其餘兩扇後面則是山羊。
你選擇了一道門,假設是一號門(猜中機率1/3)
然後知道門後面有什麼的主持人,開啟了另一扇後面有山羊的門(為增加遊戲刺激與趣味性,主持人開的一定是山羊的門),假設是三號門。
他然後問你:「你想選擇二號門嗎?」轉換你的選擇對你來說是一種優勢嗎?
Hint:
是的,主持人幫你把三個選刪去一個,只剩兩個,更換的勝算變成1/2
But 如果你本來選對,因為更換而選錯的悔恨與心理成本會增加很多...
相較於不換的1/3機率,換的猜對機率提升為2/3 (因為主持人只能挑是羊的門開)
主持人開門就是傳遞訊息- 主持人不會去開我們選擇的門,也不會去開背後是汽車的那道門=貝氏條件機率
背後的因果圖像是(衝突):你選擇的門=>打開的門<=汽車的位置
你選擇的門和汽車所在的門有假性的相依關聯
但如果主持人開門,卻不告訴你背後是汽車還是山羊,亦或主持人開門只要去開那扇不是你選擇的門(即便是有車的門也無訪)
換或不換,猜對(贏)的機率都是1/3
多數人覺得在此一遊戲當中,勝率只是從(第一階段的)1/3提升到(第二階段的)1/2 ,而非整體(兩階段)2/3
呵,拍案叫絕
人的大腦不擅長處理機率問題,出錯不足為奇
人腦很難意識到「你選的門」和「汽車所在的門」有關聯性
更多衝突偏差:柏克森悖論
Berkson's paradox
指的是兩個本來無關的變量之間,出現看似強烈的相關關係。
e.g., 女生覺得有魅力的對象脾氣差,個性好的對象沒有魅力
實際上是
1.女生交往對象的選擇第一志願是有魅力+脾氣好,第二志願有魅力或脾氣好,不會跟沒有魅力and脾氣差的對象交往
2.事後的詮釋偏誤
3.魅力與脾氣其實兩個因素彼此獨立無關
魅力=>擇偶<=脾氣
一般民眾罹患骨骼疾病的比例約7.5%,此疾病比例和呼吸道疾病無關
然而在罹患呼吸道疾病住院的病患中,罹患骨骼疾病的比例提高到25%
骨骼疾病=>住院<=呼吸疾病
不夠謹慎的研究者,為了抽樣方便,選擇住院的研究者(sampling bias),導致觀察到此一假性相關(當然也可以解釋住院的都是體質弱的,存在體質這個干擾因素)
辛普森悖論
Simpson’s paradox
兩個變量似乎相互之間具有正相關(說),而實際上它們具有負相關性,則是由“潛伏”混雜因素引起的。
辛普森悖論面在決策中具有以下兩難選擇的實際意義:
決策應參考的是分類分區的數據資料還是彙總的數據資料?
當條件未知時,在一種情況下以及在其否定情況下均優選的治療也應被優選。
另一方面,如果要先驗地優先使用分區數據,那麼什麼會阻止人們將數據分區為人為地構造為錯誤選擇治療方法的任意子類別(例如,基於眼睛的顏色或治療後的疼痛)?
在很多情況下,提供正確選擇操作的是匯總數據,而不是分區數據。更糟糕的是,給定同一張表,有時應遵循分區的數據,有時還要遵循聚合的數據,具體取決於數據背後的故事,每個故事都有自己邏輯。
1.某藥物對於降低心臟病有效果
2.此藥物對於男性病患反而增加風險
3.此藥物對於女性病患反而增加風險
同一種藥物怎麼可能對男性不好、對女性不好,但整體有療效?
其實辛普森悖論只是一種錯覺與誤會
1.以為因果關係可以反應統計比例上
2.此一藥物療效(effect size) < 抽樣偏誤或其他干擾因素
3.破解錯覺與誤會的方法- 要用標準差來看
4.兩組的比例與分母要相近- 以這個例子來說,女性對照組只有20人,實驗組卻有40人;男性對照組40人,實驗組只有20人
類似的棒球統計比較
因果圖- 看似性別為干擾因素
問題在於把資料合併來看不一定對,而把資料分組也不一定對!
隱藏的變項(在路徑圖上)的角色不同,結論也會跟著不同
以下藥物的案例
因果圖
研究結論
1.對於低血壓與高血壓的分組來看,藥物無效
2.看兩組高低血壓的比例,對照組高血壓的人數多(40/60),實驗組低血壓的人數多(20/60)
3.整體來看此一藥物對於心臟病而言有效(透過降低血壓的作用)
以圖畫說明辛普森悖論
運動與膽固醇的關連
破解的觀點
1.隨著年齡增長,膽固醇越高
2.運動在不同年齡層都可以降低膽固醇
3.是否運動與年齡對於膽固醇的數值而言有影響(運動的effect size
< 年齡的effect
size)
4.因果圖:
運動=>膽固醇<=年齡 (這解釋了悖論的存在)
5.倒果為因的解釋與錯覺是:運動量越高,膽固醇越高(其實是因為年紀大/三高,所以被醫師要求去吃藥+運動)
羅德悖論
什麼時候或什麼樣的問題,適合控制基線狀態已進行比較?
Hint: It depends
on your question and causal assumptions.
「相同伙食」對於男生女生的影響是否不同 (男女不是因果關係)
說法1 相同,問的問題是:「平均體重增加是否存在差異?」
1.1男女合併,看WF=WI的45度線
1.2最初體重越高,最終體重越高
說法2 不同,問的問題是:個人體重增加有哪些差異?
2.1 最初體重會影響最終體重,所以要控制最初體重來比較,看W0垂直線
2.2. 最初體重為W0的男生,其最終體重大於最初體重為W0的女生=>男生體重增幅大於女生(Hint 這是直覺的錯誤觀點)
因果圖
針對「性別」與「體重增幅」的推論
說法1是正確的=>沒有指向「性別」的後門路徑(最初體重與性別無關)
說法2 是錯誤的,應該要分來來看能男生或與女生的最初VS最終體重;而非用同樣最初體重來比較男女;用性別來區分,要注意男生人數和女生人不相等(=weighting權重不同)
說法一
不同食堂對於體重沒影響(看45度線)
說法二
有影響(控制最初體重,看垂直線)
涵義解釋
1.最初體重(WI)是影響飲食(D)與最終體重(WF)的干擾因素
2.體重輕的人傾向於到A食堂用餐,體重重的人傾向於到B食堂用餐
3.說法二是正確的,控制W0進行比較後,顯示在B食堂用餐的,體重增幅比A食堂用餐的
呵呵,這章來來回回讀了好幾次才看懂中間的微妙差異,箭頭方向不同,邏輯與涵義就不同。(難怪我的文章被審了好幾次差點不了了之,應該方法與邏輯推論把reviewer搞糊塗了,難以判定文章是有貢獻還是穿鑿附會)
第七章 超越調整:征服介入山
如何排除干擾,看見介入的效果?
手法:
後門調整
前門調整
工具變項(instrumental
variable)
最簡單的路線:後門調整公式
後門準則告訴我們該用哪一組變數以除去資料中的干擾
再由(回歸)調整公式執行去除干擾
最常見的手法
以干擾因子執行對照
e.g., 性別是干擾因子
先估計對於男性或女性的因果效應(effect size),如果男女比例不同(例如男2/3,女1/3),則取加權平均,在估計平均的因果效應
在第六章藥物案例中,介入變項-
藥物(D),結果- 是否有心臟病與一個干擾因子-性別,以上三個變數都是二元的;然而有些狀況下變項XYZ可能是連續變數,e.g., 年齡、收入、身高、體重;把連續變數切成幾個分層變數,可能會導致辛普森悖論;更糟的是:如果這種連續型的干擾變數有很多個,這些連續變數調整成類別變數,類別的項目會呈指數爆增,最後一些類別樣本數不足,無法提供機率估計值。(替代的取巧方式是「外插法」或資料fitting 的平滑函數,來處理這個維度詛咒的問題)
最常用的平滑函數就是線性近似
每個因果效應能夠以單一數字(路徑係數)代表
e.g., Y=aX+b
參數a= rYX(Y對X的回歸係數)
如果有干擾因子Z時,相關係數rYX無法告訴我們平均因果效應,只能透露平均的觀察趨勢,對策是把方程式改寫成 (神奇的簡化過程!)
Y=aX+bZ+c
係數a告訴我們Y對Z執行調整後的回歸係數(稱為部份回歸係數,寫成rYX.Z)
如果Z是唯一干擾因素,則a就是X對Y的平均因果效應。
須注意的地方
1.回歸係數有時代表的是因果效應(通常稱為路徑係數),有時則否(只是代表資料的趨勢- 稱為回歸細數)
2.回歸係數須具備以下兩點才能代表因果性
2.1路徑圖代表可信的真實狀況
2.2調整變數Z(可能不只一個)應符合後門準則
3.用回歸執行調整只能適用在線性模型,用線性模型就沒有辦法建立非線性交互作用的模式(e.g., X對Y的影響取決於Z的層級)
4.如果干擾因素無法被衡量,則此後門準則與調整公式無效
前門準則
如何正面反駁費雪?
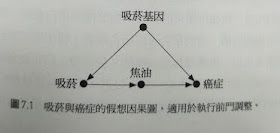
費雪邏輯的因果圖
假設
1.吸煙基因不影響焦油沉積
2.吸菸導致肺癌透過焦油(中介,也沒有其他路徑)
因為沒有辦法分析「吸煙基因」,所以沒有辦法用後門準則執行阻斷
只能走前門:「吸菸」=>「焦油」=>「肺癌」
前門的推理邏輯
1.估計「吸菸」對「焦油」平均因果效應-
觀察P(焦油│吸煙)和P(焦油│不吸煙),兩者的差異就是「吸煙」對於「焦油」的因果效應
2.估計「焦油」對「肺癌」平均因果效應
「吸煙基因」=>「抽菸」是後門路徑,可以透過控制「吸煙」 - 觀察P(肺癌│do(焦油))和P(肺癌│do(無焦油)),兩者的差異就是「焦油」對於「肺癌」的平均因果效應
3.「焦油」平均值增加的可能性源自於「吸煙」,而「癌症」平均值增加源自於「焦油沉積」,能否估算出費延源自於吸菸的平均值增加?
推理如下
3.1 癌症發生有兩種狀況- 有焦油 or 沒焦油
強迫一個人吸菸,以上兩種的機率分別是P(焦油│do(吸煙))和P(焦油│do(不吸煙)),有焦油的狀況:
P(肺癌│do(焦油));無焦油的狀況:P(肺癌│do(無焦油));依據在do(吸煙)下的機率執行加權,進而計算出吸菸導致肺癌的總機率。
靠,能夠想出這前後門方法的人真是神啊!這部份的數理統計與邏輯分析有點複雜與燒腦(欸,自己沒有本事與資質讀懂這部份)。
1853-1854 英國發生霍亂大流行,當時人們不知道致病菌/沒有人用顯微鏡觀測測微生物
霍亂發生在髒亂的地區,大家猜想:有毒「瘴氣」=>「霍亂」
Dr. John Snow懷疑以上瘴氣理論,他主張:症狀出現在腸道,一定是腸道先接觸到致病源。
好萊塢故事版
1.挨家挨戶紀錄患者死亡地點
2.注意到Broad Street 水井周圍有很多患者
3.詢問當地居民發現患者都從此一水井取水
4.別的街區來取水的也有患者
5.推論水是乾淨的,污染的是水井的把手
6.拆除掉把手後,疫情立刻緩和(實際上幫助不大)
非好萊塢故事的版本
1.同樣進行田野調查,但目的是找出倫敦的水源來自何處
2.當時水公司有A與B兩家
3.A公司的取水口在倫敦下水道的下游(受到汙染)
4.B公司的取水在幾年前移到下水道的上游(未受污染)
5. Broad Street 水井的(地下)水未受污染
6.在A公司供水區域的霍亂疫情格外嚴重,死亡率更達B公司區域的八倍
7.由於欠缺直接證據,還是沒有辦法反駁瘴氣理論支持者
因果圖如下
無法觀測到「瘴氣」這個因子,因此無法執行後門對照
然而Dr. Snow注意到:
1.A和B兩家公司的供水區域重疊交錯
2.這些用戶在「瘴氣」或「貧窮」乃至於社經地位方面,沒有差別
3.他記錄下:這是觀察與檢驗供水如何影響疫情的絕佳實驗(其實就是日後的RCT隨機對照實驗,只是剛好倫敦這兩家公司無意中成就試驗條件)
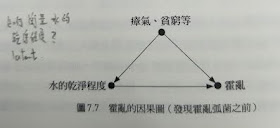
因果圖如下
Snow為本來的因果圖,引入「水公司」這個工具變項
1.由於「水公司」和「霍亂」之間沒有其他的干擾因子,因此觀察到的關連性必為因果關聯
2. 「水公司」對於「霍亂」的影響一定經過「水的乾淨程度」
3. 「水公司」和「霍亂」之間沒有直接關聯與箭頭
好膽固醇和壞膽固醇-工具變項不給力的狀況
膽固醇受當事人生活習慣/體質的干擾
另外當事人是否老實按時服藥也是大哉問
值得注意的差異是
1.我們操縱的是:病人目前的LDL值≠他/她一生的的LDL值
2.do 的計算只能找出單點估計值,而非不等性
3.然而do的計算法比工具變項更有彈性,do的計算法中不須對於因果模型中的函數性質進行假設;如果要假設單調性或線性就必須考慮工具變項
第八章 反事實:發掘可能成真的世界
因果的第一階:相關、關聯性
第二階:找出平均因果效應
隨機對照RCT
前門調整或後門調整
使用工具變項(接受線性或單調性的假設)
運用do計算法或相關的演算法
「吸菸導致肺癌」≠Joe已經吸煙三十年而得肺癌不在人世=>如果Joe 不吸煙的話,他現在會在人世嗎? (不能讓他的人生重來,來觀察比對)
指責、懊悔與歸功,背後都是因果思想的概念
人能夠想像另一個不存在的平行世界正是人與其他生物乃至於原始人的差別,能夠想像可能出現的狀況是人腦的天賦(有時候是禍害)
如何借助觀察與實驗資料,取得關於反事實狀況的資訊(登上因果的第三階)?
反事實分析能夠讓科學家提出比以往更精確的陳述,我們也需要區別三種不同的因果關係:
1.必要因果關係(必要條件) e.g., 火災的發生一定具備三要素
2.充分因果關係(充分條件)
3.充要因果關係(必要因果關係=若非因果關係) e.g., 地震導致海嘯,沒有地震就不會有海嘯
從修昔底德和亞伯拉罕,到休謨和路易斯
所多瑪城內要有多少個義人,上帝才會願意饒恕整座城的人?50個?30個?10個?
「劑量反應曲線」與「閾值效應threshold effect」是建立因果關係模型的重要資訊
休謨(David Hume)否定兩個客體之間,只要有關聯或力量,其中一者就是原因,另一者就是結果= 相關聯不是因果。e.g., 火不是熱的原因
然而對於一般人的口語陳述而言,火就是熱的原因(相關聯就是因果)
之後休謨對於因果的認定增加
1.先有因才有果的條件=>先有第一個客體,才有第二個客體
2.若無因則無果(反事實的條件)=>如無第一個客體,則無第二個客體
因果關係=若A則B(事實陳述) and 若無A則無B(反事實陳述)
如何進行反事實的演算?看到潛在的結果?
潛在結果、結構方程式,以及反事實的演算法化
用以下這個虛構的例子來看
我們只看到各種不同年資與教育程度員工的薪水,卻看不到如果他們年資/教育不同時(反事實下)的薪水(缺項)
如何推算missing data?
1.內插法技巧
2.比對 e.g., 伯特與卡洛琳年資相等但教育程度不同
3.線性迴歸
得出以下方程式:
S(薪資)=$6500+2500*EX(年資)+5000*ED(教育程度)
回歸的問題在於:
1.陳述的是相關性(因果階梯的第一層)而非因果
2.預估缺項值的依據是(回歸)模型,而非資料(無法回答第三層的反事實問題)
3.現實世界中,S(薪資)不見得會聽從EX(年資)與ED(教育程度)
假設前提
1.Awaare 學歷Ed影響經驗Ex(學歷越高,相對職場工作經驗越短)
2. 經驗Ex是學歷Ed和薪資S之間的中介變數(而非干擾變數)
3.薪水高低主要是學歷Ed、經驗Ex與未知因素Us(e.g.,
薪水特高的某人其實是皇親國戚)的函數
假設變項間是同樣的線性關係,迴歸方程式會是
S(薪資)=$6500+2500*EX(年資)+5000*ED(教育程度)+Us(其他可影響薪水但未觀察的因素unknown or observed.)
EX= 10-4*ED+Uex(其他可能影響經驗的未知因素)
接著可以找出不同員工的Us(Unique
Factor of Salary)
例如愛麗絲Us= $1000
代表她在學經歷以外的特殊因素(=績效、主管好感度或工作loading 與產出差異)
呵呵,人肉市場的標價與定價是無法做到如此科學與透明的
當資料結合以上因果結構之後的奇蹟就是:可以預測當事人(愛莉絲)在不同學經歷條件下的薪水高低
了解自己的假設是好習慣
注意以上線性因果結構模型的使用假設前提
1.穩定單位處理假設
各因素間獨立,沒有交互作用與影響(A的核薪不受B薪水的影響,實際上會)
2.一致性假設Consistency
因對果的影響具備一致性,不會今天重學歷,明天重經驗(實際上會)
3.可忽略性ignorability
學歷影響年資的部份可否忽略?如果沒有因果圖,很可能大家會掉入用學歷與年資回歸計算薪水高低的陷阱
4.可檢驗性testability
檢驗因果結構模型的推論結果是否符合真實狀況
5.自回歸的影響
薪水受去年起薪或前一份工作的影響
Y=Function (X, A, B, C, ….Uy)
6.如果要把非因果貝氏網路轉換因果模型甚至回答反事實查詢,則必須知道每個節點的劑量-反應變化關係
線性模型無法呈現非直線的劑量反應曲線,也無法呈現閾值效應
反事實與定律
反事實推論假設在法庭上非常好用
e.g., Joe堵塞了太平門,發生火災,Judy無法從太平門逃生,Judy死於火場
法律判決上:即便Joe沒有造成火災,Joe仍需為Judy的死負責
What If: 太平門沒有被阻塞,Judy就能夠存活嗎? 存活機率是多少?
如何比較太平門阻塞(X=1)與太平門沒有被阻塞(X=0)的平行時空狀態下,Judy死亡(Y=1)或沒死存活(Y=0) 的機率差異?(以驗證太平門是否阻塞是造成Judy死活的關鍵因素)
造成Judy 死亡的主力近因是火災還是太平門堵塞?
謎之聲:
火災才是造成Judy死亡的原因,太平門堵塞只不過是次要因素
What 火災是因為電線走火,電線走火原因通常是電線老舊沒有更換,而沒有更換是因為沒有標準或公司沒錢,檢察官該起訴誰?
工作場所負責人? 公司電力設備維保主管?不肯花錢修繕的董事長或財務副總?
人(官員/檢察官與法官)只能看見發生的事實與事情經過,依據證據證詞與套用法條(穿鑿附會與詮釋因果關係),所以很容易可以推定"過失"與"應為能為而不為",e.g., 發生事故是因為沒有遵守OO法規或XX規範(=找戰犯與欲加之罪何患無辭)
然而卻看不見其他可能的情境與應發生而未發生的潛在事實(反事實),e.g., 遵守了OO法規或XX規範還是會出事(只不過可能發生機率比較小),
而其他更多更兩光公司,同樣沒有遵守OO法規或XX規範,甚至更糟但卻(還)沒有出事...
謎之深因
1.出事不奇怪,奇怪的是:為什麼更多更鳥的公司還不出事?
2.從官員與檢察官”詮釋”因果關係的角度,只要出事就能找到過失,所以每個人都是天天過失與應為能為而不為,端看是否出事被起訴
3.不要跟官員或法規控爭辯適法性議題 &跟熱血憤青討論司法正義....
經典案例-「掉落鋼琴殺人事件」(並排停車導致死亡事故)
被告對受害者開槍但沒有擊中,然而受害者逃跑的過程中被掉落的鋼琴擊中致死。
控方的邏輯:被告反了殺人罪,如果被告沒有對受害人開槍,受害人不會逃跑,受害人沒有逃跑,不會被鋼琴砸中
辯方的邏輯:被告犯的是殺人未遂,應被起訴殺人罪的是吊掛鋼琴的業主或雇主的業務過失& 當事人如果跑不同方向就不會死亡了。
造成Y死亡的主力近因是X開槍還是Z鋼琴掉落?
法院判決通常依據近因原則,而且責任歸屬交由法官的直覺來認定…
幾種情境
A. X=0 Y=0 可以想像,也沒有爭議:X沒有開槍,Y不中槍/不會逃跑/不會被鋼琴砸中
B. X=1 Y=1 的機率? X開槍,Y中槍受傷死亡 符合一般邏輯/爭議小
C. X=1 Y=0 的機率? X開槍沒中,Y躲開 符合一般邏輯/爭議小
D. X=1 Y=1 X開槍沒中,Y逃跑到鋼琴下的機率 爭議大
E. X=0 Y=1的機率? X沒開槍,Y自己路過被鋼琴砸死 背景機率
從貝氏機率(反事實常理)的角度看
A>B>C>D>E or A>B>C>E>D?
關鍵在於D跟E的機率哪個比較大
如果Y遭遇橫禍的機率本來就很高(e.g., 美食外送員),是否死於此一離奇意外其實沒有差別(死了就是死了,X不是導致Y死亡是主要的contributing factor)
如果Y死於橫禍意外的機率很低,而且在當時情境下,Y只能逃到鋼琴吊掛處下方或衝向火車鐵軌,那麼X是主要的contributing
factor
X是否是導致Y死亡的主要contributing
factor,it
depends on:
1.Y當時有沒有其他逃生動線
2.X的槍與槍法準不準,不準的話,Y不逃說不定反而沒事
3.X有沒有殺Y的意圖或動機或者反過來Y自己有沒有埋下X的殺機(X是被討債的好人,Y是壞人,鋼琴掉下來是上帝鏟奸除惡的旨意)
主力近因的定義相當模糊,從因果的關係,要看充分條件(Sufficient Conditions)與必要條件(Necessary Conditions)
行刑隊有AB兩人,兩人開槍都足以導致囚犯死亡
A或B開槍只是導致囚犯死亡的充分條件,但非必要條件
A開槍導致囚犯死亡的充分機率PS是:1-Pa(開槍-失手的機率Pa)
A開槍導致囚犯死亡的必要機率PN則取決於
1.B沒有開槍的機率
2.B開槍但失手的機率
從機率與反事實的角度來看,主力近因=充分機率
X開槍,造成Y跑到鋼琴底下的機率為何? 如果X開槍,而Y跑到鋼琴底下的機率很低,則不能說X開槍的這個動作,導致Y被鋼琴壓死
火柴點火造成房屋火災
1.沒有點燃火柴,房屋就不會燒燬
2.沒有氧氣,房屋就不會燒燬
點燃火柴造成房屋燒毀=>充分機率與必要機率都很高
氧氣造成房屋燒毀=>必要機率很高但充份機率很低
法律沒有明確區分充分機率與必要機率,乃至於兩者的比重
必要原因、充分原因和氣候變遷
2003/08 500年來最強的熱浪侵襲西歐,導致法國1.5萬人死亡,許多是沒有空調的獨居老人。
他們是全球暖化的受害者? 還是只是在錯誤的時間出現在錯誤的地方?
Myles Allen
Liability for Climate Change, Nature 2003
透過”可歸因危險分子Fraction Attributable Risk,
FAR” 來估計氣候變遷的(對於導致這些人死亡的)效果
計算出2003熱浪發生的氣候變遷(AD1800)之前的機率P0
與氣候變遷(AD1800)之後的機率P1
如果P0=1/1000
P1=2/1000,則我們有一半的風險是因為氣候變遷(危言說法:增加一倍)
如果P0=1/1000
P1=3/1000,則我們有2/3的風險是因為氣候變遷(危言說法:增加3倍)
FAR的計算=充分機率PS,就以下兩個寬鬆的因果假設下
1.處理(溫室氣體)和結果(熱浪)兩者間未有其他干擾因素
2.溫室氣體增加主要變因是人類的活動
3.在沒有干擾與防護的條件下,氣候變成變成導致人受熱浪侵襲死亡的必要機率PN
如何驗證以上FAR的估計?
電腦模擬
Human Contribution to the European Heatwave
of 2003
https://www.researchgate.net/publication/8149698_Human_Contribution_to_the_European_Heatwave_of_2003
模擬結果顯示:FAR超過50%的機率是90%
白話翻譯:以CO2濃度而言,現在發生類似2003夏天熱浪的機率,是工業革命前兩倍以上的可能性是90%以上
兩層的不確定敘述
第一層氣候變遷的不確定性,我們估計的信心度約為90%
第二層氣候變遷的幅度,我們估計約為50%(=兩倍)
氣候變遷的因果圖
Causal counterfractual theory for the
attribution of weather and climate-related events.
估計顯示
充分機率PS很低約0.0072=>代表當年度難以預測到該事件
但必要機率PN約0.9=>代表溫室氣體導致類似事件發生的機率很高
而充分機率PS必須放在更長的背景時間尺度下觀察,我們不只想預測今年是否造育類似熱浪,更想知道未來5年、10年或50年再次遭遇類似強大熱浪的機率
200年內歐洲遭遇類似熱浪的機率是80%,二氧化碳濃度持續提高會使PS不斷提高=縮短下次熱浪來襲的間隔。
學術研究大哉問:
該不該相信電腦模擬的結果?對於該結果有多大的信心度?
氣候學家依靠的是近百年的資料建立氣象模型,這些模型有做過未來百年氣候變化的預測與前瞻性試驗來驗證嗎?
2010熱浪襲擊莫斯科,兩個團隊得不同結論
一個團隊斷定造成熱浪原因是自然變異,認為CO2濃度是PS,造成熱量主因是當時氣候的持續高壓壟罩俄羅斯
另一個斷定造成熱浪原因是氣候變遷,以PN為觀點
作者認為氣候條件與CO2濃度都是充分條件PS,只不過不同的研究團隊著眼於不同的PS。
Hint:
就工安事故而言,人犯錯與設備故障通常是直接原因(必要條件PN)=>看當下
而組織管理不當與資源不足是釀成人犯錯與故障的間接原因和底層脈絡(充分條件PS)=>看長期或然率
事故的究責與檢討要看必要條件(PN)還是充分條件(PS)?必要條件(PN)的責任多一些還是充分條件(PS)的責任多一些?
反事實的世界
充滿驚奇,我們只看到多個平行時空下的一種事實結果,看不到其他可能的事實結果,也只能透過想像、試驗與電腦模擬去猜測反事實的樣貌,乃至於用各種難以直觀理解的統計機率與數學函數陳述,來表達各種平行時空的樣貌。





















沒有留言:
張貼留言