因果革命:人工智慧的大未來
The Book of Why: The New Science of Cause
and Effect
前情提要
機率不等於因果關係
相關性不等於因果關係
討論因果關係的方法
外行人班門弄斧/造口業該被打屁股,來好好反省+讀一讀真正大師的見解
自序
這本書的目標有三個:
1.以非數學語言讓讀者理解因果革命的詳細內涵,以及它將如何影響我們的生活和未來。
2.為讀者介紹科學家遭遇及挑戰關鍵因果問題時,英勇解決的歷程。
3.把因果革命帶回人工智慧的最初本源,介紹如何讓機器人學習以我們的母語(即因果語言)溝通。
人的思想與邏輯為何如此運作?因果、榮譽與遺憾、意圖與責任的意義是什麼?
前言:思想勝過資料
腦中的邏輯與因果推論(思想)詮釋了真實世界當中發生的事情(資料)
科學≒因果推論(causal
inference)
這種新科學可以處理這些看似簡潔明瞭的問題:
‧某種療法預防疾病的效果如何?
‧是新稅法使得銷售增加?還是那是打廣告的結果?
‧醫療成本中,有哪些可歸因於肥胖?
這些問題都和因果關係有關,特徵是「預防」、「使得」、「歸因於」、「政策」,以及「應該」等這些詞。這些詞在日常交談中經常使用,社會也經常得回答這些問題。但直到非常近期,科學都沒有提供任何方法來清楚表達這些問題,更不用說解答它們了。主要的阻礙是:我們用來描述因果問題的詞彙,與傳播科學理論時使用的傳統詞彙,基本上有所差異。
想像科學家試圖表達某些顯而易見的因果關係時,有多麼困難,例如氣壓計讀數為B時,代表大氣壓力為P。我們可以輕易寫出像B = kP這樣的方程式,其中k代表某個比例常數。接下來可以依據代數法則,把這個方程式隨意改寫成各種形式,例如P = B/k、k = B/P,或是B – kP = 0。這些方程式的意義全都相同,只要知道這三個量中的二個,就可求出第三個量。k、B和P這幾個字母在數學上的地位,都不比其他字母高。那麼我們又該怎麼表達我們相信是壓力造成氣壓計讀數改變,而不是氣壓計造成壓力改變?如果我們連這麼簡單的因果關係都無法表達,又怎能表達其他連數學公式都沒有的因果概念?(例如太陽升起不是因為公雞報曉的關係。)
數學等號左右兩邊可以置換,沒有因果關係概念
但隨著科學好奇心逐漸增長,我們也開始在複雜的法律、商業、醫學和政策制訂場合提出因果問題,我們發現手上沒有成熟科學應該提供的工具和原理。因果理論需求開始浮現之際,統計學也在此刻誕生。事實上,正是高爾頓和皮爾森對遺傳產生疑問,巧妙地運用跨世代資料來解答這些問題,才孕育出現代統計學。可惜的是他們沒有問為什麼,而是宣告這些問題無法回答,同時開發與因果性無關的興盛學科,稱為統計學。統計學告訴我們「相關不是因果」(Correlation is not causation.),卻沒有說因果到底是什麼。在統計學教科書的索引裡你找不到「原因」。不講X是Y的原因,只能說X和Y「相關」或「有關聯」。
由於這樣的禁忌,統計學認為不需要數學工具來處理因果問題,它在意的只有如何總結資料,而不是如何詮釋資料。唯一的例外是1920年代遺傳學家西瓦爾‧萊特發明的路徑分析(path analysis),這也是本書許多方法的鼻祖。然而路徑分析完全不受統計學和相關領域青睞,因此停滯在萌芽階段數十年之久。統計學的其他領域,包括想求助於因果推論的其他學科,也還處於禁忌時代,誤以為所有科學問題的答案都蘊含在資料中,可以透過巧妙的資料探勘技巧發掘出來。資料本位的歷史至今仍然揮之不去。然而資料本身是中性與中立的,端看當事人如何詮釋或解釋。
探討因果關係的三種語法
一、知識語言:因果圖(Causal Diagram)
點 代表變量(variable) , 線與箭頭 代表已知或可能存在的因果關係
e.g.,
雞鳴=>日出 or 日出=>
雞鳴
可能存在許多穿鑿附會或倒果為因的誤謬
二、數學(統計)語言:貝氏機率
想知道某種藥物(D)對於病患壽命(L)的影響=>想知道服用D這種藥物的病患,活L年的機率:P(L│do(D) )
臨床上還要解盲確認藥效>安慰劑效應= 比較P(L│do(D) )和 P(L│do(not-D) )
然而在數學上
把自願服用D藥物患者的預期壽命L的可能性寫成P(L│D )
P(L│D
) 和 P(L│do(D) ) 兩者看似相同,然而前者是「觀察到某個現象」,而後者是「刻意造成此一現象」
e.g., 蘋果橘子經濟學
健康的人少上醫院看醫生P(L│D ),還是民眾為了避免染病而不上醫院P(L│do(D) )?
消防隊越多/火警意外報案件數越多P(L│D
),市政府為了減少火警/意外事件數,裁撤消防隊P(L│do(D)
)
分析因果的訣竅在於:說明如何不需實際介入,就能預測這項介入的效果
三、反事實語言(counterfactual):What If
e.g., 如果病患服用藥物D之後,一個月後死亡,能不能驗證探討導致病患死亡的是不是跟此一藥物有關?
換言之,What If病患沒有服用此一藥物,他會不會活下來?
e.g.,
從統計語言的角度,只知道「雞鳴」與「日出」兩者間有關聯性,無法判別因果
反事實語言:雞鳴,太陽沒有出來或沒有雞鳴,太陽照樣出來=>確認兩者不相干
反事實的推論能力構成了人類的道德與科學思維,從過往行為現象反推其他狀況的能力士自由意志和社會責任的基礎;而會思考的機器與強AI需要的正是此一能力。
理解現實的邏輯藍圖
1.知識是虛線框代表隱藏在推理者腦中,推理者與模型不見得能完整表達與陳述自己的知識
2.科學研究依據知識提出簡化的假設,後續的因果模型其實就是一連串的假設。提出假設的方式與好壞對於驗證假設、從假設驗證中獲得結論甚至獲得證據修改或拓展假設有深遠的影響
3.因果模型,可使用因果圖、SEM、邏輯敘述等來表達
4.因果模型上的路徑,應該在資料中形成觀察得到型態或相依性dependency;沒有路徑相連的在統計學的陳述為”相互獨立”。如果資料獲得呈現的形態與以上涵義相互牴觸,代表因果迷型假設必須修改,估算資料和模型間的適配(degree of fitness)
5.最後,如果模型正確,資料充足,便可獲得因果查詢的答案。e.g., D藥物可使糖尿病患的壽命延長30%,上下誤差20%。如果驗證不順利,至少也可以提供一些建議,說明造成D藥物不給力的可能原因。
新的科學趨勢是跳過現有知識與假設來建模,而直接透過人工智慧與機器學習來建立因果模型;作者對此一大數據的作法持保留態度,原因
- 無法回答「如果採取不同行動會如何?」,機器與人工智慧建模只能fit data pattern,無法解釋或說明模式的樣態
- 以上模型是data dependent,換一個地區、產品或族群就有不同的pattern=沒有適應性/無法累積智慧;傳統的假設模型會有參數估計與了解變數間的關連性,換個地區、產品或族群,只要調整各參數的數值或獲得新的預測參數=有適應性
- 人類比資料聰明,模仿自己就是了解自己的最佳方法(而不是透過機器去proxy)
第一章 因果階梯
創世紀 亞當與夏娃的故事
上帝問”What (do
you do)” (釐清事實)
亞當和夏娃回答的是”Why
(I do it)” (試圖獲得原諒與寬恕)
神話故事背後的涵義
1.人類知悉世界不單只有事實與現象,還知道各種事實與現象之間有錯綜複雜的因果關聯
2.構成知識的主體要素是因果推論與解釋,而非單純的事實陳述
3.人的智能由單純的資料處理(刺激=>反應)轉變解釋的提供者,過程不是漸進而是跳躍的。機器不可能從資料中獲得解釋,它需要助力。
求生狩獵需要計算與規劃,規劃計算=在腦海中想像與模擬,想像與模擬需要設定因果關係;想像可以跳脫現實與天馬行空
人類大歷史
自私的基因(關於意識的出現)
意識究竟從何而來?
因果的三個層級
第一個層次是觀察 探知環境中的規律
歸納出規律
e.g., 生物基本的計算與模仿能力
目前的大數據與機器學習停留再此一階層:回歸、找出相關性
辯認出各種物體、語音與臉孔
第二個層次是 實行與試誤嘗試 刻意改變各種條件或變數,看看能不能得到想要的成果?
測試出這些規律的適用性與效力大小
無法單靠觀察得到答案
e.g., 使用工具與做出計畫,如果調高售價,產品銷售量會如何變化?
科學知識起源於實驗組與對照組;所謂的經驗=長年觀察的推論(不用靠試誤就可以猜出介入的結果)
第三個層次 想像不存在的世界與不同的情境,推知各種現象背後的因果關聯
推理出未知情境的狀況
人只能觀察到發生的事實,無法告訴我們某些以知事實或條件改變時的狀況。
不斷嘗試與累積各種不同條件狀況下所得的規律=定律
讓我們從歷史與他人的經驗中學習
想想出不存在的世界=藝術創作,也是各種科學理論、發明與創新的基礎,能夠想像才能夠變成真實
迷你圖靈測驗
圖靈測驗
如何只用一個字證明你是人還是機器人
機器很難通過圖靈測試的原因
1.人的大腦有很多預測的機制與範本(感情、同理)
2.假設有十個變項,每個變項輸出只有1和0可能變化有3000萬個=>變項更多、輸出更複雜=可能組合多到超乎想像
3.人腦習慣於用因果圖,但機器很難用因果圖進行邏輯運作
4.人腦可以回答反事實規則的問題,但機器無法跳脫運算規則(=無解);人腦善於打破規則,電腦不善於打破規則
5.人腦可以理解「只是觀察事件」和「介入造成事件」兩者間的差別,對於機器而言,兩者的運算邏輯不同。
更複雜的狀況下,人腦也一樣很難做出正確的因果結論
e.g., 接種天花疫苗
疫苗剛問世時,死於接種疫苗的人數多過於感染天花而死的人數
假設有 100萬兒童
99%接種,1%沒有接種
接種的兒童中1%出現天花反應,反應導致死亡的機率是1% (9900人出現天花,死亡99人)
沒有接種的,感染天花的比例是1/50,死亡率是1/5(200人出現天花,死亡40人)
新聞報導標題- 疫苗殺人
接種疫苗喪生百人,未接種疫苗死亡40人(公衛官員下台,父母抗拒帶小孩接種)
反事實推論
如果接種率是0,結果會是如何?
100*1/50= 2萬感染,2萬*1/5=4000人死亡,死亡人數少了4000-99-40=3861人
因果圖的神奇
1.把問題或故事敘事轉成因果、填入相關已知資訊或知識、進行反事實推論與比較
2.因果概念比統計更容易讓人理解(人類理解的是因果,而非機率),傳遞的訊息比統計更容易讓人接受
3.因果圖的結構在此一案例中不會改變,需要改變的只有各種估計參數
機率與因果
一般生活用語
因果的第一個層級- 觀察到的關連性
機率提高=因果,用機率來定義因果
e.g., 喝酒(X)開車會出車禍(Y),不認真(X)唸書會被當(Y)
因果邏輯:X導致Y
誤區
X與Y之間的共同因素可能才是真因
e.g., 冰淇淋的銷售量(X)和犯罪率(Y)成正比,不是吃了冰淇淋會讓人想犯罪,而是天氣熱(Z)導致冰淇淋銷售量(X)增加與人心浮動的犯罪(Y)
透過條件機率或者介入與否差異來修正機率與定義因果
因果的第二個階層- 找出各種變因間的關連
透過消除各項背景干擾變因,來呈現X與Y之間的因果關聯(but 仍是用機率來呈現因果)
用機率來說明因果性,像一艘船,只要碰到未知的背景干擾變因就會沉沒
拯救機率因果性的方法是:說明
P(Y│do(X) )> P(Y
) =>有了介入的差別,由機率是否顯著提高來說明確認X是不是Y的原因
哲學觀點的因果關係
- 因的出現早於果
- 有因必有果 ,因果伴隨
- 反事實條件關係(有因沒果 or 沒有因的時候,果會不會也不發生)
- 充分條件、必要條件
- 因果關係意味著可預言性的規律,但是這種可預言性不意味著實際與未來的必然性,因為沒有人可以知道一切相關的事實與背景干擾因素,從而因果關係的預言性也就包含了錯誤的可能性
經濟學方面的研究
透過 格蘭傑因果性(Granger Causality)
與 向量自我回歸(Vector Autocorrelation)
來說明因果關係與解決部份統計機率上的缺陷
機率代表的是過去的抽樣結果乃至於心目中對於世界的想像與預期
而因果邏輯指引我們的是:當世界因想像或介入而改變時,機率是否發生改變與如何變化
欸,這本書應該會要反覆看好幾遍,才有辦法稍稍體會與領域作者的思想
第二章
從海盜到天竺鼠:因果推論的創生
看這章之前,可以複習一下 統計改變了世界
Francis Galton
受到堂兄查爾斯·達爾文(Charles
Darwin)1859年出版的《物種起源》的影響,探索人口變異及生物受“馴化下的變化”。
他猜想卓越與智慧會遺傳,結果發現所謂卓越人士的上一代與下一代沒那麼卓越,上上一代跟下下一代其實更平庸。
一開始稱以上現象為逆轉(reversion),後來改為”回歸中庸regression toward
以為這是某種遺傳定律,其實不過是統計現象
遺傳有變異,為什麼人的身高沒有出現270公分 的巨人和70公分 的矮人?
他的(錯誤)解釋- 有某種機制會限制第二代的身高繼續發散(想了8年,沒有想到那個機制為何)
但是進一步研究,他又發現
爸爸如果比較高,而兒子通常比較矮;兒子如果比較矮,孫子通常比較高
更趣味的是:可以用父親的身高來預測兒子的身高,也可以用兒子的身高來預測父親的身高(遺傳上的因果關係顛倒)
 |
| OM是已知父親身高時,兒子身高的預測線。 ON是已知兒子身高時,父親身高的預測線。 |
法蘭西斯‧高爾頓捨「因果」而擁抱「相關」
高頓原本追尋的是「因果」或「遺傳定律」,結果發現無視於因果的「相關」
他的學生Karl
Pearson再提出回歸線斜率的公式,稱為相關係數(correlation coefficient, r)
決定係數(R-Square)與相關係數(r)之間的迷思
在直線回歸的情況下 r的平方= R-Square
相關係數(r)測定與表述的是兩變數間的直線性關係(非線性或圓形, r=0)
決定係數(R-Square)
測定與表述的是回歸方程式(可以是線性或非線性)的解釋力與適配性
後見之明
中央極限定律與向均值回歸
回歸均值可謂是種錯覺,常態分布與回歸均值也只適用在部分領域!
- 均值之所以為均值,就是有的比它大、有的比它小(總體分配向平均值靠攏),回歸均值不是自然法則,只不過是統計現象與狀態
- (從時間縱斷面與遺傳來看)特別大的值= 基因因素+ 外在環境與機運影響,外在環境與運氣因素不見得可以持續=回歸均值(好運要代代相傳,身高才會越來越高)
- 物競天擇,離群點=異常,異常=生存條件不佳=沒有機會傳宗接代=回歸均值
- 身高取決於基因,而基因會趨於穩定與平衡,變異不會無限發散 Hardy–Weinberg_principle https://en.wikipedia.org/wiki/Hardy%E2%80%93Weinberg_principle
- 除了看回歸之外,還要觀察散佈的狀況(散佈的越開=相關性越差,用父親的身高來預測兒子的身高,r與R-Square都沒有很漂亮,代表背後沒有掌握的因素很多影響解釋力高)
- 「相關」是「因果關係」的「必要條件」:具備因果關係的兩個變數,一定高度相關;有相關不見得有因果關係,換言之如果相關性不高,不必奢言具備因果。
卡爾‧皮爾森把「因果」掃出統計學
科學的文法
「以往一再出現的某種結果是一種經驗,我們以因果概念表達這種經驗…..然而科學無法證實這種經驗或結果的必然性,也不可能完全證明它一定會一再出現」
因果關係就是完美的相關!
皮爾森是實證學派(熱衷於馬克思的資本論也覺得自己像是個海盜- 可以無視各種既有規則),認為外界事物都只是人類思想的產物,科學只是這些思想的表述,人腦中認定的因果關係不是客觀過程的科學,用「相關」的概念比因果更客觀與科學(試圖把因果概念從科學中拔除)。
生物統計學期刊成為他個人化的期刊;然而尷尬的是:他自己寫過幾篇假相關(spurious correlation)的論文,一定要藉因果概念才能理解。
e.g., 人均巧克力食用量與該國諾貝爾獎人數明顯相關(橫斷面)
年度死亡率和在教堂舉辦婚禮有相關(時間縱斷面)
更有趣的是隨便混合兩組資料(
男女頭顱的長度與寬度)也會出現顯著相關
辛普森矛盾(Simpson’s
paradox)
只能透過因果與邏輯來判斷與解釋:什麼時候可以合併資料、什麼時候不該合併資料(=分群分析)
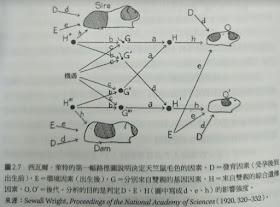
萊特、天竺鼠和路徑圖
熱愛數學與天竺鼠的Sewall
Wright
(詮釋因果關係的)路徑分析
1920年,他研究的問題:
為什麼天竺鼠的毛色完全不服從孟德爾的遺傳定律?
假設天竺鼠的毛色受到以下因素的影響
D發育因素(受孕到出生前)
E環境因素(出生後)
H親代的遺傳因素
最後證明猜想- 發育因素比遺傳因素更重要
在隨機培育的天竺鼠,毛色型態的變異42%出自遺傳,58%出自發育
在近親繁殖的天竺鼠當中,3%變異出自遺傳,92%是發育
路徑圖的科學革命與美妙
- 跨過因果階梯的第一層,進入第二層(不單只是觀察,還有做出嘗試與驗證)
- 他沒有宣稱路徑圖理論可以提供通用做法來推論因果關係,然而透過結合因果推論與統計數據可以獲得某些結果。「相關意味著具備某些程度的因果關係」
- 估算因果效應的強度(路徑係數Path coefficients are standardized versions of linear regression weights which can be used in examining the possible causal linkage between statistical variables in the structural equation modeling approach.由某個變項解釋的變化量或介入對於來源變量產生的效果)
- 圖上畫出與看得見的箭頭沒有說明效應大小,而沒有劃出的箭頭則意味者忽略的假設(假定因果效應為零,加以忽略;然而說不定更重要)
- 把顯而易見的假設搭配上20+年累積的資料得到難以看見的定量結果(毛色型態的變異42%出自遺傳,58%出自發育)=>結合完全不相容的「圖形語言」和不相容的「資料與數學語言」
- 科學家當然不可能再事前完全知悉所有變數之間的關係脈絡,因此可以透過假定的因果關係路徑來進行預測,如果預測路徑結果與實際資料相牴觸,代表假設的關係脈絡有錯,應該進行修正。
1953 Herbert Simon 使用類似路徑圖的方式,於1978獲得諾貝爾經濟學獎
皮爾森學派對於這篇論文的批判
1.把因果關係和相關
兩者相提並論,毫無根據與意義
2.這個圖形系統是事前給定,真實狀況符合此一系統假設?
3.統計就是客觀的資料彙整,而非僭越的詮釋因果
E PUR SI MUOVE(但地球依然在轉動)
宗教法庭強迫伽利略收回地動學說,他的喃喃自語
萊特前無古人,也不受當代皮爾森學派的接納,隻手建立了現代因果分析的新典範
1921年發表的論文
相關與因果關係
路徑分析的數學邏輯演繹- 數學連結因果與相關
為什麼路徑(因果)分析沒有獲得重視、引發風潮?
1.統計思考不鼓勵科學思考(帶入因果主觀偏見)
2.進入因果分析前,必須瞭解產生資料的過程與說明資料以外的知識。
3.費雪(跟皮爾森一樣固執)把萊特當成對手,否定其觀點與演化生物學的基因漂變(drift)理論
重新被發現但卻走鐘與面目全非的路徑分析
路徑分析被社會科學家改名為結構方程式建模(SEM)
1970電腦軟體LISREL問世,研究者變成軟體操作者(亂發問卷)
SEM與因果性無關(因為使用共變細數矩陣進行分析)
題外話:
1.搞不懂SEM的八大矩陣+沒有學通矩陣向量,自己是SEM外行(雖然也當過一陣子SEM分析操作的人型喪屍)
2.聯想到HLM,其實HLM的邏輯也不是因果,而是作用與影響力
3.好多的研究都是用SEM,理論上不應該那麼多的顯著與剛好fit預先設定的model,難怪很多研究成果沒有辦法複製與重現...(學術悲哀與醜聞)
在經濟學中,路徑分析的代數部份變成聯立方程式模型
這些方程式沒有方向性,難以分辨是因果還是相關,乃至於背後的雞生蛋/彈生雞
使用這些方程式解答做出政策決策的,往往難以說明結果的因果含意乃至於反事實意義
萊特的終極一戰與兩種科學哲學觀點
Samuel Karlin
反對路徑分析的理由
- 兩個變數間的關係為線性=>非線性理論即將問世,可以解決此一問題
- 可以用無模型的方式來理解資料,對於結果的解釋更Robust
- 對於統計學家而言,談的是客觀的相關與資料如何歸納,而非主觀的因果
萊特的反駁
- 應該被捍衛的是:科學方法與詮釋資料的基礎
- 「無模型」方法,能夠讓人驗證因果階梯的第一階- 相關性,但無法讓人更上一階 (很容易觀察到的是偽相關性)
- 沒有理論基礎與對於因果關係的知識不應該進行分析
兩位大師秉持不同科學哲學觀點,爭辯可謂是雞同鴨講
也只有大師間的爭辯才會直指科學哲學的核心,不會在方法與文章標點的枝微末節上打轉
貝氏連結將主觀機率帶進統計學界
結合觀察證據/數據與以往經驗知識/主觀想法
拋擲一枚硬幣10次,其中9次出現人頭,請問下一次出現人頭機率為何?
- 統計學新生:1/2 or 50%
- 統計魔人:9/10 or 90% (沒有輔助證據,只能相信先前數據結果)
- 貝氏派觀點:要看當時被老千的可能性與情境(可能是1/2 或9/10)
兩種對立 科學哲學的爭辯
客觀統計
- 資料是可觀的,意見是主觀的,資料比意見或詮釋重要
- 採用的是機率與數學語言
- 資料量增加,但對於因果的主觀偏見不見得會隨時間而消失:相信兩種不同因果主張的兩派人馬可以分析相同資料,但永遠不會得到相同的結論
- 因果關係是人腦當中根深蒂固的一種錯覺
主觀因果
- 分析不應該只是一些陳規式的描述,而必須帶入各相關專業領域的知識與程序(說明文獻回顧與Argument
- 採用的是圖像語言(路徑圖)
- 隨著資料量增加,逐漸篩除各種不符合資料的想法,理論上可以獲得客觀的結論
- 只要大家對於假設前提有共識,就能客觀的來詮釋資料或證據,也才能修正既有誤解或偏見,獲得新知識。
兩種截然不同的觀點與科學典範,其實兩種語言- 不論是統計/數學 亦或 因果/影響
都需要花腦力。
有心上進的學弟在FB上分享自己買的新書,出於善意把這本書也推薦給他;現在想想果然是造孽與造成他的困擾:學習也需要審美觀與美學,審美觀與美學有三個層次
1.鄉民的層次,能夠理解背後的道理與邏輯,欣賞這個道理與邏輯的美感與簡潔
2.操作的層次,知道這些邏輯與道理透過什麼樣的工具與方法或獲得,乃至於操作過這些工具與方法
3.行家的層次,看懂人家如何推導與架構這些知識與邏輯,乃至於拍案叫絕,自己怎麼沒有辦法亦若是。








沒有留言:
張貼留言