因果革命:人工智慧的大未來(書名副標翻譯的不好/畫蛇添足)
The Book of Why: The New Science of Cause
and Effect
作者Judea Pearl
2002年
兒子Daniel Pearl在巴基斯坦被綁架並被謀殺,帶領猶太和家人及朋友的其他成員創建了丹尼爾·珀爾基金會,為猶太人和穆斯林之間的和解而努力。
信奉遵從猶太傳統但卻不相信上帝的存在
他在UCLA的網頁
Dana Mackenzie(科普作家)
本書為博班等級的教材當之無愧(事實上也是),不少內容需要動手做計算與補修相關知識(能夠把因果關係講清楚的老師不多,不少reviewer其實是一知半解的造業作虐之半吊子外行)
第三章從證據到原因:當貝斯遇見福爾摩斯
演繹:一般通常是從推論產生結論:假設=>證據驗證=>結論
規納:證據=>假設=>結論 (反過來從證據產生假設)
福爾摩斯:「排除所有不可能之後,剩下的即便再不可能,也一定是真相」
貝斯牧師與逆機率問題
Thomas Bayes
神學與數學間的大哉問:
需要多少的證據,才能讓人相信- 某件不太可能的事情(e.g., 耶穌復活)真的發生過?我們憑什麼理由認為各種週期秩序或現象會穩定與恆常,而非源於機率的巧合與不規則性?
Hint(辨證邏輯):
我們不太知道耶穌復活這件事是否為真,如果這件事真(儘管機率很低),那麼我們越應該相信造成他復原的原因(=相信上帝的存在)
正向機率
知道造成某個結果或現象的原因,從原因出現推算發生某個原因或結果=>相對容易
e.g.,
已知屁孩把球丟向窗戶,請問窗戶被打破的機率?
知道球桌長度,想知道球撞出去,會停留在距球桌左端小於X英呎的機率?
Hint: 球桌長度是12英尺,停留在球桌小於X英呎處的機率= X/12
逆向機率
推估特定結果為某個原因所導致的機率=>相對困難(要排除各種可能解釋)
e.g.,
已知窗戶被打破,請問原因是屁孩的機率?
已知球停留在小於X英呎處,請問球桌長度L的機率?
茶點館的案例
2/3的客戶點了茶P(T),其中1/2點了司康 P(S│T)….(1)
5/12的客戶點了司康P(S),其中4/5點了茶P(T│S)….(2)
點了茶又點司康= P(T)*
P(S│T) = 2/3*1/2=
1/3 ….from(1)
點了司康又點茶= P(S)*
P(T│S) =
5/12*4/5= 1/3…from(2)
涵義:
1.客戶點餐的順序不重要
2.如果客戶點了司康,可有更高的信心度推測(4/5)與可推薦他/她點茶
3.如果客戶點了茶,相對他/她會再點司康的信心比較低(1/2)
以上推論的兩大缺陷
1.理論缺陷:
把機率解釋成信心度! 信心度或可信度不見得= 資料出現的比例
不能把我們已知(的數據與抽樣結果),轉換成機率語言,乃至於主觀的信心度(如同擲骰子10次,人頭出現9次,再次出人頭的機率不見得是9/10,信心度也不見的是9/10)
2.實際缺陷:
事前的機率猜測夾雜個人主觀性(subjectivity),不同的人依據各自片段的經驗,事前預測的機率值可能差異非常大,另外看似主觀的貝氏機率推論,如果能夠加入因果方向的資訊,能夠幫助決策更精準
年紀40歲左右的女性,乳房X光檢測顯示罹患乳癌,該不該進行手術?
檢測的偽陰性與偽陽性
3000位檢測
其中2996位結果顯示OK(沒有乳癌徵狀),但其中360位最後顯示有乳癌(偽陰性)
4位顯示有疑慮的,其中3位真的有乳癌,另一位虛驚(偽陽性)
篩檢工具評估方法(敏感度/精確度/偽陰性/偽陽性)
https://www.hpa.gov.tw/File/Attach/1213/File_371.pdf
是否真有乳癌需要該開刀邏輯思維
- 實際上可能罹癌的機率:4/3000=0.13% (每700人才有一個乳癌,客觀/大數法則)
- 醫師問診+觸診:是否有家族病史+可能病徵,才考慮是否進行進一步的檢測(主觀區別)
- X光檢驗,but還是有很高的誤判機率(把有判成沒有的機率是1/4;把沒有判有的機率是12%)=>X光檢測 篩出363/3000= 約12%的人有疑慮
- 主觀先驗機率*概似比(Likelihood ratio)= 修正的機率(信心度)
- 概似比(Likelihood ratio)= P(T│D)/ P(T):陽性檢測的敏感度(正確性)/ 總檢測12率= 75%/(4/3000*75%+2996/3000*12%)= 75%/ 12%= 6.25
- 主觀先驗機率(0.13%)*概似比(6.25)= 0.81%(陽性預測值),換言之,檢測結果為陽性,該女性罹患癌症的機率仍然小於1%,可謂每100人當中就有99人虛驚一場)
- 可以再做組織抽樣確認,或乾脆依病人意願採取預防性切除(硬塊腫瘤其實是良性的,病人冤旺白挨一刀)
結論:
40歲以上女性,不需要因為害怕乳癌而每年作X光檢驗(因為誤判虛驚比例太高,乃至於依據誤判結果,採取治療誤割乳房…)然而很多菜籃族不理解背後的風險與機率邏輯,抗議沒有幫忙做好健康管理與早期發現、早期治療…
題外話:
想到以下新聞
女星利用基因檢測,發現自己帶有乳癌基因BRCA1的變異,為了免於罹患乳癌,毅然決定接受「預防性乳房切除手術」。不知道她有沒有想清楚與理解各種檢測的誤判風險...(有錢就是任性,而有錢與任性不代表有智慧)
貝氏方法的美妙
1.把「就我已知」的經驗主張,轉化為統計語言,以數學展現個人經驗(或猜測依據)
2.提出假設
3.依據該假設演繹出可檢測的結果
4.作實驗、檢測與收集證據
5.依據實驗與檢測結果的證據,修正我們對於假設的置信度
6.證據不是肯定或否證假設,現實與科學當中的證據都帶有一定的不確定性
7.透過以上流程,讓我們可以從因果的第一階朝向第二階邁進
直觀理解貝式定率及其應用(超神的資料科學網站)
先驗客觀基率(該地區的每年下雨機率/一般人罹癌機率)+之後資訊與主觀判斷
從貝氏法則到貝氏網路
貝氏網路
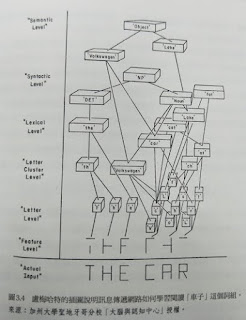
機器學習的人工智慧,必須仿照人腦的資訊處理- 透過不同階層的神經元(階層式神經網路)來進行理解與閱讀
由低而高的階層
1.圖像
2.字母
3.單字
4.文法
5.語意
由上而下(由親節點傳往子結點)傳遞資訊時,子結點運用同條件機率更新置信度
由下而上(由子節點傳往親結點)傳遞資訊時,親結點依據自己原來的置信度*概似比(likelihood ratio)更新成為新的置信度
由下而上與由上而下的兩個法則,反覆套用在網路中的每個節點,稱為置信度傳播(belief propagation) https://en.wikipedia.org/wiki/Belief_propagation
貝氏網路與機械學習
貝氏網路:原因透露了哪些關於資料的線索?
以上討論過的貝氏網路(兩個節點一個箭頭,箭頭方向可以相反)
茶=>司康
疾病=>檢查
三個節點兩一個箭頭的情況
1. A=>B=>C(鏈chain) B是把A的影響傳遞給C的中介變數
e.g., 起火=>冒煙(或溫度上升)=>火警 ,起火本身不會傳警告(除非當場有人目睹)
知道「起火」的值(發生機率),不會降低或提高對於「火警警報(偵測器)」的置信度;「警報」的輸出只有1或0
我們要知道警報的誤警率(被灰塵干擾)或可靠度(有95%的時間正常作用,5%時間不會發揮作用- 斷線沒電),才知道該對「警報」有多大的置信度
「起火」與「警報」兩者之間可謂是條件獨立(conditionally independent) if 沒有中介的冒煙(或溫度上升);另外警報是否發出,也要看(it depends on)該偵測器是否妥善維護
(呵呵,難怪很多警報大家視而不見當成狼來了)
2. A<=B=>C(分叉 fork)
B是A和C的共同原因或是干擾因子
e.g, 鞋子尺寸<=兒童年齡(成長)=>閱讀能力
可以把B條件化,以消除此類假性相關
e.g., 只比較同年齡的小朋友(的閱讀能力)
已知(或控制)B時,A和C兩者為條件獨立(conditionally independent)
3.A=>B<=C (衝突 collider)
e.g., 才華=>成名<=外貌
才華或外貿都可以讓明星演員成功
對於一般大眾而言,才華與外貌兩者是條件獨立(conditionally independent)
然而相對於明人而言,通常有才華的外貌普通,有外貿的才華普通,A和C兩者相互衝突(自原其說效應 collider bias)
鏈、叉與衝突三種連接方式,像是鑰匙孔,透過它們窺視讓人得以看見分隔因果關聯的第一階與第二階
原因和機率之間的聯結就是貝氏網路對於因果推論科學最大的貢獻。
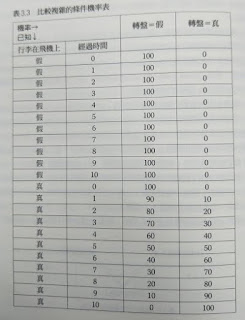
我的行李在哪裡?從亞琛到尚吉巴島
等的越久沒看到行李出現在行李轉盤,行李出現的機率越低(=越可能遺失)
真實世界中的貝氏網路
波拿巴軟體
如何從關係較遠親屬的DNA轉換成貝氏網路,以判定罹難者的身分
手機通訊
把聲音轉成01編碼,但傳地接收過程可能產生錯誤- 把1判成0,把0判成1
修正錯誤的方法
加入額外資訊,e.g., 把1編碼成111、0編碼成000
如果收到編碼101,會修正成1
以上做法的缺點- 訊息長度變成3倍/沒有效率
改良方式:
1993 Claude Berrou https://en.wikipedia.org/wiki/Claude_Berrou
發明 Turbo Code
把每段資訊編碼兩次,第一次直接編碼,第二次把資訊打斷後再編碼,產生兩組不同的碼字,接收方解碼時套用置信度傳播的方式在此一貝氏網路上,99.999%會產生正確的資訊位元(錯誤率十萬分之ㄧ)
解碼效率越好,代表通話品質、使用時間與鬼地方都收得到訊號
從貝氏網路到因果圖
因果圖與貝氏網路的差別
貝氏網路結合因果圖和資料數據
置信度傳播的演算法,在因果圖中仍然成立
貝氏網路其實是一堆變數之間 關聯性與機率的呈現
因果圖上的箭頭,僅代表子代節點與親代節點代入特定方程式數值的機率,此為充分條件(非必要),如果兩節點間沒有箭頭,代表這兩個節點相互獨立
ABC三個節點間的關係可以是 A=>B=>C 代表B僅探尋A,C僅探尋B;A由模型外的力量或因素決定;而模型可以變成C=>B=>A,A和C條件獨立的狀態不變,但結構中的因果讀值將大幅改變
從貝氏網路傳達的兩個重要意義
1.因果假設不能任意創造,必須受到資料檢驗,而且可能遭到推翻
2.因果圖的圖形特性,說明了哪些因果模型能由資料區分,哪些模型無論資料量再龐大都不能區分
e..g, A跟C獨立,然而從資料(變數間的關連性上)無法驗證區分因果邏輯是A=>B=>C or
A<=B=>C
3.要區分以上兩種因果圖路徑,不能只靠觀察資料,要進行實驗與介入,看看增加A(或控制B不變)時,C是否跟著A增加(如C跟著增加,則因果邏輯圖是A=>B=>C;如C沒有增加,則因果邏輯圖是A<=B=>C)
貝氏網路無法區別「觀察」與「介入」的差別
討論與處理因果關係的幾種方法
- 隨機控制實驗(RCT)=>舊科學與傳統統計認可方法,可謂只是某種推論因果的特例(適用在部份情境下,特別是自然科學)
- 觀察相關性與共變性(社會科學與經濟學),乃至於透過時間序列變化先後來論斷因果
- 介入觀察(縱斷面)與實驗操弄(橫斷面)
- 貝氏網路=>人工智慧與資料處理
第四章 干擾與去干擾:或說剷除潛在變項
史上最早的對照組與實驗祖研究紀錄- 聖經 但以理的故事(BC 597)
吃素會不會影響奴隸服侍巴比倫國王的能力?
不吃葷的奴隸但以理提議:
吃素和吃葷各挑四人,連續飲食10天,10天以後比較兩組人的胖瘦
對照實驗Controlled Experiment
實驗組(Invention)
vs 控制組(Control)
史上最著名的失敗對照實驗研究-
Hawthorne Studies
成功地開啟了心理學與社會學研究的新大陸
對照實驗最大的不確定因素- 干擾confounding
醫學-藥物效用研究中常見的干擾因素
安慰劑效應、年齡、運動習慣、種族、心理信仰、飲食習慣…..
干擾因素對於統計(不談因果)與分析資料相關性而言,(因果階梯第一階的關聯)是大災難
然而對於進入因果階梯的第二階-
介入驗證而言,卻是不可或缺的一部份
如果能夠控制以上干擾因素,其實就可以大膽表示X對Y的因果效應(effective size)
去除干擾的方法
1. 正統
統計標準典範- 隨機對照試驗RCT
2.後門準則 back-door criterion (1990年代問世)
干擾導致(陳述因果時的)強烈恐懼
從8000人中選出707人當樣本
12年後,偶而步行者(每日走不到1.5km ),死亡率43%
經常步行者,死亡率21.5%
研究者知悉年齡是干擾因素,調整年齡因素後
偶而步行者(每日走不到1.5km ),死亡率41%
經常步行者,死亡率24%
大自然的巧妙質問:隨機對照試驗為何有效用?
費雪女兒的陳述:
大自然回答我們的問題,但答案搖擺不定也模擬兩可人類問題的目標是找出因果規律或效力,但妨礙達成目標的主因就是干擾
1923-1924 費雪逐漸發現,要讓大自然這個精靈答其所問的問答方式,就是隨機實驗
費雪知道:問題如果正確,但答案不確定(效果不顯著),也比問題不正確但答案很明確要好得多(虛假的顯著效果)
隨機化的好處
1.消除干擾因素(向大自然提出正確的問題)
2.量化不確定因素(或說量化在不確定因素干擾下所呈現的肥料效力)
90+年後,透過因果圖來看費雪的問題
 |
| 模型1:沒有適當的隨機控制,直接比較兩塊地有無施肥的差異 |
 |
| 模型2:同一塊地,直接比較有無施肥時的差異(沒有被去除的干擾因素是年度氣候/甚至當年度有無除草) |
 |
| 模型3:透過抽紙牌來隨機指定施肥的土地,再比較兩群土地產量的差異 |
去除干擾的新典範
如何明確定義干擾?
我們觀察到的某個結果(變量Y),是已知在某個狀態或介入-X下的條件機率:P(Y│X )
我們想了解的是X跟Y之間的因果關係:X=>Y
這個關係是人為介入,所以條件機率應該寫成:P(Y│do(X) )
干擾的定義不過就是造成 P(Y│do(X) ) ≠ P(Y│X ) 的因素s
白話:
如果事先猜想可能存在干擾因子,就應該調整(此干擾)因素,進行試驗,之後再於去不去除干擾的情況下進行試驗,如果前後兩者有差異,代表存在干擾因子。
敘述性定義
1.一般口語:干擾因子是同時與X和Y相關的變項
2. 流行病學:變項Z是X(處理)和Y(結果)的干擾因子相關的變項,此變項Z
2.1 在群體中與X相關
2.2 在未接受X處理的群眾中與Y相關
2.3 Z不應該位在X和Y的因果路徑上(不是中介變數)
流行病學定義的罩門
1.必須要有很強力的理由相信Z跟X無關
2.Z說不定是中介變數M的代理(proxy , 因為M無法直接被測量)
e.g., 「政黨參與」被當成「政治信仰」的代理
程序性定義
臨床實證常識行定義
3.從反事實(其他可能狀況)的角度來看,「Z在群體中與X相關」and 「在未接受X處理的群眾中與Y相關」既不充分也不必要
e.g.,有人打了流感疫苗卻染病(不打沒事),有人沒打流感卻沒有發病(身體有抵抗力產生抗體)
X(打疫苗)=>Y(罹患流感)
p有預防成效的理想狀況:X=1 => Y=0;X=0 =>Y=1i沒有預放成效(受試群體已有抗體/免疫):X=1 => Y=0;X=0 =>Y=0c打了反而致病(疫苗毒性太強):X=1 => Y=1;X=0 =>Y=0d 有打沒打都染病 (疫苗沒效):X=1 => Y=1;X=0 =>Y=1
只有當p, i, c, d相仿時才代表兩組交換,不會沒有太大結果差異與複雜干擾因素(e.g., 性別、年齡、健康狀況、可能影響的人格特質或生活習慣差異)存在
do運算子和後門準則
因果圖如何把「干擾」這個頭痛問題變成趣味遊戲?
可以把因果圖的箭頭,想像成:資訊從起點X傳送到Y的管道
資訊的傳遞包含因果和非因果兩個方向,非因果路徑的資訊傳遞=干擾
在鏈
A=>B=>C,以B執行對照,可以防止A的資訊傳遞至C
在分叉或干擾的連結
A<=B=>C,以B執行對照,可以防止A的資訊傳遞至C,也可以阻止C的資訊傳遞至A
在衝突A=>B<=C,以B執行,反而A與C之間的資訊會相互流通
去除干擾=阻斷資訊傳遞的後門,但不阻斷或干擾因果路徑
遊戲1
X:吸煙,Y:流產, A:吸煙導致的內在異常(無法觀測), B:過往的流產史
B其實不是干擾,只不過是中介變數A的proxy=>所以不需要執行對照
如果對B執行調整,會導致低估吸煙對於流產的影響
遊戲2
X:母親目前是否吸煙(第二胎孕期),A:母親第一胎是否吸煙,B跟E:吸煙導致的潛在異常(無法觀測);D:造成這些異常的其他因素,C上一胎是否流產
ABCD可以視為「處理前變項」,有條後門路徑X<=A=>B<=D=>E=>Y
應針對A執行對照條件化或甚至不執行對照(後門被D卡住)
A跟C要能夠同時調整(C是B的量測proxy)
遊戲3
後門路徑X<=B=>Y
必須對B執行條件化
然而如果B無法接觀察,只能透過A proxy,對A執行條件化意義不大(說不定會造成新的干擾),則一定要進行隨機對照實驗RCT
=> Y=1;X=0 =>Y=1
遊戲4 M bias
如果B變項同時跟X和Y相關就叫干擾,其實是一種誤會
e.g., 繫安全帶(B)對於抽菸(X)和肺癌(Y)沒有關係
而是繫安全帶(B)反應出當事人對於社會規範(A)和關心個人健康 (B)的態度(=間接測量)
遊戲5
事實上,是否繫安全帶(B)跟是否抽菸(X)有關
可惜當事人對於社會規範(A)和關心個人健康 (B)的態度無法直接測量,也難以進行對照,以B執行對照其實是錯誤=>會導致XABCY之間的連通
比較建議用李克特量表衡量C,進而條件化C
遊戲1-3 的出處
Clarice Weinberg, Toward a Clearer
Definition of Confounding, 1993
遊戲4跟5的文章出處:
Introduction to causal diagram for
confounder selection, 2014
尋找釐清因果關係是一種遊戲與樂趣,遊戲的背後困惑了多年的問題與嚴肅的研究苦工
第五章 煙霧瀰漫的爭議:除去迷霧
1950-60期間,統計與醫師的大哉問:「吸菸是否會導致肺癌?」
反對意見的最佳說法:有不明因素會同時導致尼古丁成癮與肺癌
以往的因果研究的幸運典範
1747 James Lind透過受控的對照試驗,發現壞血病由缺乏維他命C造成
1849/1855 John Snow 使用統計數據來說明水源質量與霍亂病例之間的聯繫。
維他命C與霍亂弧菌分別是造成壞血病與霍亂之間的充分且必要條件
吸煙致癌挑戰了以上因果概念
有人沒吸煙卻罹患肺癌,有人終身吸菸卻沒罹患肺癌
打破因果爭辯僵局的Austin
Bradford Hill
希爾準則- 每一條都可以有例外也非必要條件,但整體而言極具(因果推論)參考價值
摘錄:
1.強度(效果大小):小的關聯並不意味著沒有因果關係,儘管關聯越大,則因果關係的可能性就越大。
2.一致性(可重現性):不同地區,不同地點,不同樣本的不同人觀察到的一致發現會增強效果的可能性。
3.特異性:如果在特定部位和疾病中有非常特定的人群而沒有其他可能的解釋,則可能是因果關係。因素與效果之間的關聯越具體,因果關係的可能性就越大。
4.臨時性(時序性):後果必須在原因之後發生(如果原因和預期結果之間存在預期的延遲,則後果必須在該延遲之後發生)。
5.生物梯度(劑量-反應關係):更大的接觸通常應導致更大的效應發生。但是,在某些情況下,僅存在因素可能會觸發效果。在其他情況下,則觀察到相反的比例:更大的暴露導致更低的發生率。
6.合理性:因果之間的合理機制是有幫助的(但希爾指出,該機制的知識受到當前知識的限制)。
7.連貫性:流行病學和實驗室檢查結果之間的連貫性增加了影響的可能性。但是,希爾指出:“……缺乏此類[實驗室]證據無法消除對協會的流行病學影響”。
8.實驗:“有時可以訴諸實驗證據”。
9.類比:在觀察到的關聯與任何其他關聯之間使用類比或相似性。
10可逆性:如果原因被刪除,那麼效果也應消失。
菸草:人為流行病
菸草銷售量與男性肺癌死亡的關聯
然而與肺癌/菸草銷售同步相關的因素還有:空氣污染、汽車銷售、含鉛汽油與柏油鋪設
希爾知道,無法使用RCT試驗來釐清香煙與肺癌的關係,只能間接比較已罹癌和健康受訪者的差異-
Case Control Study (1948)
649名罹癌的病患,只有兩名不吸煙
優點:
1.比前面只看時間序列相關性的那種好
2.能夠以年齡、性別、接觸污染物等背景干擾因子進行對照
缺點
1.回溯式:已經得癌症才來找原因(戰犯)
2.資料呈現的是- 癌症患者的吸煙機率,而非吸煙者得癌症的機率
3.受訪者回憶偏差(研究者調查的是吸菸造成肺癌,受訪者就說吸菸造成肺癌)
4.抽樣偏誤,住院的肺癌患者不等於所有人,甚至無法代表吸煙族群
儘管類似的對照研究在其他國家進行了19次,費雪批判:有偏差的實驗進行19次一樣沒意義(1957)。
研究設計/studydesign101
Case Reports=> Case Control Study=> Cohort
Study=> Randomized Controlled Trial=> Practice Guideline=> Systematic Review=>
Meta Analysis
杜爾與希爾在1951年進行前瞻性研究
發送問卷給六萬名 醫師,調查吸菸與否,接著進行追蹤
1956 明顯的差異出現:
重度吸菸者的死亡比例是不吸菸者的24倍
吸煙越多,罹患癌症的風險越高,戒菸則可降低風險- dose-response effect≒因果關係
然而費雪還是質疑以上研究的證據力- 認為有不明因素(e.g., 基因)會同時導致尼古丁成癮與肺癌
題外話:2000年人類基因完成定序,發現費雪既是對的也是錯的:真的有基因與肺癌有關,but影響力不大
對於費雪體質假說,傑爾姆·康菲爾德與亞伯·利連菲爾德於1959年共同發表了一篇論文,逐一駁斥了費雪論述。假設存在一個混雜因子,比如吸煙基因,它完全地解釋了吸煙者患肺癌的風險。如果吸煙者患肺癌的風險為常人的9倍,那麼在吸煙者中,這種混雜因子存在的概率也需要至少比常人高出9倍,如此才能解釋這種患病風險的差異。
這意味著:如果有11%的不吸煙者攜帶“吸煙基因”,那麼就至少有99%的吸煙者一定攜帶吸煙基因。而如果有12%的不吸煙者碰巧攜帶這種基因,那麼從數學的角度看,“吸煙基因”就不可能完全解釋吸煙和癌症之間的相關。對生物學家來說,這個被稱為“康菲爾德不等式”(Cornfield's inequality)的論證瓦解了費雪的假說。
香菸論戰是科學家面對刻意欺騙的對手
1.冥頑不靈與僭越的學術大咖- 費雪(可惜他沒得肺癌,否則不知他內心作何感想…但他值得尊敬的是- 自己吸菸&沒有收菸草公司的經費)
2.刻意隱瞞與欺騙大眾的煙草公司
衛生總署委員會和希爾準則
1962 The Royal College of Physicians 首先發難,斷定吸煙是肺癌的致病原因。
1963美國衛生總署的顧問委員會研究如何評估吸煙的因果效應
William Cochran (Pearson 的再傳弟子)
報告寫道
統計方法無法證明關聯中的因果關係,關聯中的因果顯著性是(主觀)判斷問題,無法以統計機率說明;要判斷疾病間的關果顯著性或是對於健康的影響,必須運用準則:
- 一致性(在不同群體中進行的多項研究,結果相仿)
- 關聯強度(劑量-反應效果,劑量大風險高)
- 關聯特異性(特定因素導致特定效果,而非導致各種不同效果)
- 時間關係(原因在效果前)
- 連慣性(生物可信和吻合實驗室細胞研究)
結合以上四點,希爾綜合以上論點以便套用在其他公衛問題,希爾稱這些準則為「觀點viewpoint」而非規定,任何一點都不是必要條件
成為跳脫統計,接受某個因果假設的典範
吸菸對新生兒的影響
出生體重悖論
1959年,研究舊金山灣區15000兒童的產前與產後資料,包含母親吸煙習慣、新生兒的重量與第一個月的死亡率
先前的研究指出,若母親吸煙,則嬰兒出生時的平均重量低於不吸菸者的嬰兒
另外出生重量過低的嬰兒(<2.5kg),死亡率是體重正常嬰兒的20倍
研究前猜想的因果鏈:吸煙=>出生重量低=>死亡率
結果發現:
1.若母親吸煙,則嬰兒出生時的平均重量低於不吸菸者的嬰兒
2.母親吸煙的嬰兒,存活率高於母親不吸煙的嬰兒(吸菸有益)
Hint:
有個叫做出生缺陷的因素,影響了存活率
激烈爭議:科學與文化
相較於白人,黑人女性更容易生下體重過輕的小孩,嬰兒死亡率也較高
但黑人生下體重過輕的小孩,期存活率反而高於白人生下體重過輕的小孩
納入種族這個因素,引發歧視爭議,應該處理的是造成黑人嬰兒死亡率偏高的社會問題(社經地位低下),而非把問題推到種族上
因果圖的語言讓人得以冷靜看待原因和結果,無論是否面對文化與社會爭議。



















沒有留言:
張貼留言